笔者最初学习的时候,对于”把某某曲线沿着 轴旋转一周“类的题目有些茫然。本文将图文并茂,彻底带读者搞清楚这个问题。
此类题型可能要求求抛物线、双曲线绕某个轴旋转一周形成的曲面方程。
当一个曲线绕x轴旋转时,每个点的坐标和z坐标将形成一个圆的方程,其半径等于原始y坐标的绝对值。也就是说:
r怎么确定呢?由于该曲线位于平面上,所以曲线上任意一点在开始旋转时的y值就是半径。故有:
所以只需要把曲线中的替换为即可解出新的曲面方程。
同理,绕y轴旋转时,的值为半径,所以有:
注意,要看清题目中曲线位于哪个平面上,再确定半径为多少。对于平面上的曲线,替换方程略有不同。这里不做展示:
- 绕轴:
- 绕轴:
- 绕轴:
这张图演示了平面上的抛物线绕x轴旋转180度的图像。右边是正面视角,不难看出:
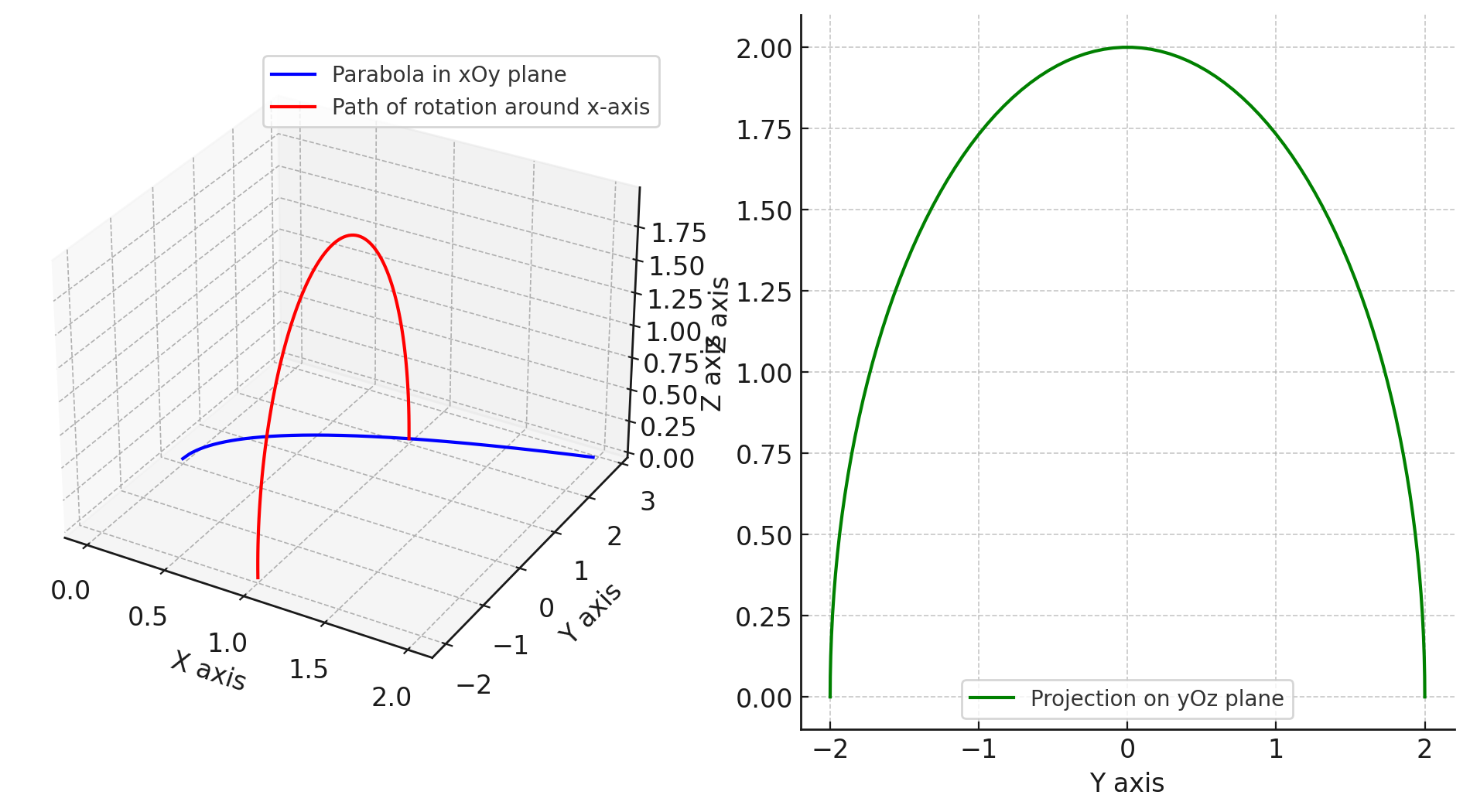
为方便记忆r值,可以这样理解:要从x,y,z三个值中选一个作为r,只需要先去掉所绕的坐标轴,再选取剩下两个值与平面两个值的交集。
例如, 平面上某曲线绕 轴旋转,去掉x轴,还有y,z。再求y,z与x,y的交集,得出r为y。